TI-84 Plus: Bézier Curves
The Bézier Curve is defined as a set of parametric equations of n points:
x(t) = ∑( nCr(n,r) * (1-t)^(n-k) * t^k * x_k ) from k = 0 to n
y(t) = ∑( nCr(n,r) * (1-t)^(n-k) * t^k * y_k ) from k = 0 to n
For 0 ≤ t ≤ 1
The curve fits points (x_0, y_0) (when t = 0) and (x_n, y_n) (when t = 1). The degree of the polynomial is n-1.
This blog covers the TI-84 Plus. I have a version for the TI nSpire and HP 50g which can be found here:
The arguments given for the BEZIER program are two lists: one of x-coordinates and one for y-coordinates. The program switches to Parametric mode.
In order to accomplish this, I store lists to equation variables, convert them to strings, and build a string to be converted to the equation.
The commands Equ>String and String>Equ are found in the catalog ([2nd] [ 0 ]). The DelVar command can handle one variable at a time. Temporary variables (XT5, YT5, XT6, YT6, Str7, Str8, Str9, Str0) are deleted at the end of the program to save space.
Program BEZIER
Disp "BEZIER CURVE"
Input "X=",L₁
Input "Y=",L₂
If dim(L₁)≠dim(L₂)
Then
Disp "LISTS NOT SAME LENGTH"
Stop
End
Param
dim(L₁)→N
seq(K,K,0,N-1)→L₅
seq(N-K-1,K,0,N-1)→L₆
seq((N-1) nCr K,K,0,N-1)→L₄
L₄*L₁→L₃
L₄*L₂→L₄
"L₃"→X₅T:Equ>String(X₅T,Str7)
"L₄"→Y₅T:Equ>String(Y₅T,Str8)
"L₅"→X₆T:Equ>String(X₆T,Str9)
"L₆"→Y₆T:Equ>String(Y₆T,Str0)
"sum("+Str7+"*(1-T)^"+Str0+"*T^"+Str9+")"→X₁T
"sum("+Str8+"*(1-T)^"+Str0+"*T^"+Str9+")"→Y₁T
0→Tmin
1→Tmax
.05→Tstep
DelVar X₅T:DelVar Y₅T
DelVar X₆T:DelVar Y₆T
DelVar Str7:DelVar Str8
DelVar Str9:DelVar Str0
ZoomFit:Zoom Out
Examples:
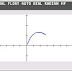
Example 1: (0,0), (1,2), (3,1)
X List: {0,1,3}
Y List: {0,2,1}
Example 2: (-2,4), (0,0), (2,4), (4,2)
X List: {-2, 0, 2, 4}
Y List: {4, 0, 4, 2}
Example 3: (0, 10), (1, 6), (3, 3), (5, 8)
X List: {0, 1, 3, 5}
Y List: {10, 6, 3, 8}
This blog is property of Edward Shore. 2016
TI-84 Plus: Bézier Curves
 Reviewed by Anonymous
on
12:57
Rating:
Reviewed by Anonymous
on
12:57
Rating:
 Reviewed by Anonymous
on
12:57
Rating:
Reviewed by Anonymous
on
12:57
Rating:









No comments: