HP 71B: Simpson’s Rule Approximation for f(x,y)
Happy New Year everyone! Hope everyone had a great New Years Day! J
For the TI-84 Plus version, please visit here: http://edspi31415.blogspot.com/2016/02/ti-84-plus-simpsons-rule-for-fxy.html
Today, I will present apply the Simpson’s Rule to functions of two variables like f(x,y) for the HP 71B. Here is the general algorithm:
Start with the function f(x,y) and your integration limits A, B, C, and D.
Then determine Δx and Δy (labeled E and F in the programs below) by:
Δx = (B – A)/(N – 1)
Δy = (D – C)/(N – 1)
Where N is the number of partitions. Unlike the Simpson’s Rule for one variable, in this case N must be odd. Generally, the higher N is, the more accurate the approximation is, with the expense of additional computational time.
Next, build a matrix, let’s say [ I ]. This is your Simpson’s Matrix. The Simpson’s Matrix is built by the expression
[ I ] = [1, 4, 2, 4, 2, 4, 2, 4, 2, …, 4, 1]^T * [1, 4, 2, 4, 2, 4, 2, 4, 2, …, 4, 1]
The length of the vector used to determine [ I ] depends on N. A way to build it by the routine:
Store 1 into the element 1 of [ I ] (first element)
Store 1 into the element N of [ I ] (last element)
For J from 2 to N – 1
If J is divisible by 2, then store 4 in the jth element of [ I ],
Else store 2 in the jth element of [ I ]
For N = 5, the vector would be built is [1, 4, 2, 4, 1]
And
[ I ] = [1,4,2,4,1]^T * [1,4,2,4,1] =
[[1, 4, 2, 4, 1]
[4, 16, 8, 16, 4]
[2, 8, 4, 8, 2]
[4, 16, 8, 16, 4]
[1, 4, 2, 4, 1]]
Build another matrix [ J ]. The elements are determined by the following formulas:
For row j and column k, the element is f(A + Δx*(j – 1), C + Δy*(k – 1))
Once finished, multiply every element of [ I ] by [ J ]. This is NOT matrix multiplication. Then sum all of the elements of the results. In essence:
S = ∑ (j = 1 to N) ∑ (k = 1 to N) [I](j,k)* [J](j,k)
Determine the final integral approximation as:
Integral = Δx * Δy * 1/9 * S
The program DBLSIMP uses N = 5. This program works best for f(x,y) where they are polynomials. On the HP 71B, matrices cannot be typed directly, elements have to be stored and recalled on element at a time. The program presented does not use modules.
HP 71B Program DBLSIMP
At least 580 Bytes
Edit f(x,y) at line 10. Use variables X and Y.
5 DESTROY I,J,A,B,C,D
8 DESTROY E,F,K,S,X,Y
8 DESTROY E,F,K,S,X,Y
10 DEF FNF(X,Y)= [ enter f(X,Y) here ]
12 RADIANS
14 DIM I(5,5)
20 I(1,1) = 1
21 I(1,2) = 4
22 I(1,3) = 2
23 I(1,4) = 4
24 I(1,5) = 1
25 I(2,1) = 4
26 I(2,2) = 16
27 I(2,3) = 8
28 I(2,4) = 16
29 I(2,5) = 4
30 I(3,1) = 2
31 I(3,2) = 8
32 I(3,3) = 4
33 I(3,4) = 8
34 I(3,5) = 2
35 I(4,1) = 4
36 I(4,2) = 16
37 I(4,3) = 8
38 I(4,4) = 16
39 I(4,5) = 4
40 I(5,1) = 1
41 I(5,2) = 4
42 I(5,3) = 2
43 I(5,4) = 4
44 I(5,5) = 1
50 DISP “X: from a to b” @ WAIT 1
52 INPUT “a = “; A
54 INPUT “b = “; B
56 DISP “Y: from c to d” @ WAIT 1
58 INPUT “c = “; C
60 INPUT “d = “; D
62 E = .25 * (B – A)
64 F = .25 * (D – C)
66 S = 0
70 FOR J = 1 TO 5
72 FOR K = 1 TO 5
74 X = A + E * (K – 1)
76 Y = C + F * (J – 1)
78 S = S + FNF(X,Y) * I(J,K)
80 NEXT K
82 NEXT J
90 S = S * E * F/9
95 DISP “INTEGRAL = “ @ WAIT 1
97 DISP S
Examples:
F(X,Y) = 2*Y – 3*X
A = 1, B = 2, C = 2, D = 5
Result: Integral = 7.5
(Actual answer: 7.5)
F(X,Y) = X^2/Y^2
A = 1, B = 2, C = 2, D = 5
Result: Integral ≈ 0.70212579101
(Actual answer: 0.7)
F(X,Y) = 0.5*X*EXP(Y)
A = 1, B = 2, C = 2, D = 5
Result: Integral ≈ 105.942243008
(Actual answer is about 105.768077253)
Source:
Cooper, Ian. “Doing Physics With Matlab: Mathematical Routines” School of Physics, University of Sydney
Retrieved January 30, 2016
Thank you, and wishing you a happy, healthy, and successful 2017!
Eddie
This blog is property of Edward Shore, 2017
HP 71B: Simpson’s Rule Approximation for f(x,y)
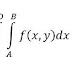 Reviewed by Anonymous
on
20:18
Rating:
Reviewed by Anonymous
on
20:18
Rating:
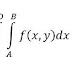 Reviewed by Anonymous
on
20:18
Rating:
Reviewed by Anonymous
on
20:18
Rating:







No comments: