Right Triangle: Finding the Dimensions Knowing Only Area and Perimeter: finding a general formula
Problem: Given the area of a right triangle (R) and perimeter (P), find the dimensions of the right triangle (a, b, and the hypotenuse c).
Three facts about right triangles:
(I) Area: R = 1/2 * a * b
(II) Perimeter: P = a + b + c
(III) Pythagorean Theorem: a^2 + b^2 = c^2
The task is to find a, b, and c:
Step 1:
Of (I):
1/2 * a * b = R
a * b = 2 * R
Step 2:
Then from (II):
a + b + c = P
a + b = P – c
Step 3:
Squaring both sides:
(a + b)^2 = (P – c)^2
Step 4:
Expanding the left side:
a^2 + 2*a*b + b^2 = (P – c)^2
2*a*b + a^2 + b^2 = (P – c)^2
With a^2 + b^2 = c^2 (III) and a*b=2*R (Step 1):
2*(2*R) + c^2 = (P – c)^2
Simplify:
4*R + c^2 = P^2 – 2*P*c + c^2
4*R = P^2 – 2*P*c
c = (P^2 – 4*R)/(2*P)
Step 5:
Rearrange (I) to solve for a (we could solve for b but the procedure is similar)
1/2 * a * b + R
a = (2*R)/b
Step 6:
Use (III) and Step 5 to solve for b:
a + b + c = P
a + b = P – c
(2*R)/b + b = P – c
2*R + b^2 = b*(P – c)
(at this point, c is known)
b^2 – b*(P – c) + 2*R = 0
Using the quadratic formula:
b = ( (P-c) ± √((P-c)^2 – 8*R) )/2
In conclusion:
c = (P^2 – 4*R)/(2*P)
b = ( (P-c) ± √((P-c)^2 – 8*R) )/2
a = (2*R)/b = P – a - c
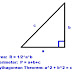
Example:
Given R = 6 and P = 12
c = (12^2 – 4*6)/(2*12) = 5
b = ( (12-5) + √((12-5)^2 – 8*6) )/2 = 4
a = 12 – 5 – 4 = 3
c = (12^2 – 4*6)/(2*12) = 5
b = ( (12-5) - √((12-5)^2 – 8*6) )/2 = 3
a = 12 – 5 – 3 = 4
Solutions:
a = 3, b = 4, c = 5
or
a = 4, b = 3, c =5
Eddie
This blog is property of Edward Shore, 2016
Right Triangle: Finding the Dimensions Knowing Only Area and Perimeter: finding a general formula
 Reviewed by Anonymous
on
19:30
Rating:
Reviewed by Anonymous
on
19:30
Rating:
 Reviewed by Anonymous
on
19:30
Rating:
Reviewed by Anonymous
on
19:30
Rating:







No comments: