Bessel Function of the First Kind
The program BESS1 calculates the Bessel function of the First Kind. With the HP Prime and Casio Classpad, and any calculators that can process integrals (and the processor is fast enough), we can use the definition:
J_n(x) = 1/π * ∫ (cos(n*t – x*sin(t)) dt for t= 0 to t = π
This is the solution to the differential equation:
x^2*y’’ + x*y’ + (x^2 – n^2)*y = 0, where y is a function of x.
There are many other variations and approximations to calculate J_n(x) if the integral function is not available on your calculator.
More information on the Bessel function is found here:
Wolfram
Wikipedia
Casio Classpad (fx-CP400): The Function BESS1
As the screen above shows, I used a Define statement in the Main Mode:
Define bess1(n,x) = 1/π ∫ (cos(n*t – x*sin(t)) dt, from t = 0 to t = π)
Note: Make sure that the calculator is in Radians mode before calculating.
HP Prime: BESS1
EXPORT BESS1(n,t)
BEGIN
// Bessel 1st Kind
LOCAL b;
// Integrate
b:=(1/π)*CAS.int(COS(n*X-t*SIN(X)),X,0,π);
// Approximate
b:=approx(b);
RETURN b;
END;
Examples
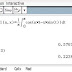
bess1(1,2) ≈ 0.576724807756
bess1(0,6.3) ≈ 0.223812006132
bess1(2,4) ≈ 0.364128145852
This blog is property of Edward Shore, 2016.
HP Prime, Casio Classpad: Bessell Functions of the 1st Kind
 Reviewed by Anonymous
on
06:08
Rating:
Reviewed by Anonymous
on
06:08
Rating:
 Reviewed by Anonymous
on
06:08
Rating:
Reviewed by Anonymous
on
06:08
Rating:







No comments: